AC 自动机¶
概述¶
给定一堆关键字和一篇文档,AC 自动机可以在文档中快速查找出所有的关键字匹配。算法复杂度为 O(n),n 为文档的长度。AC 自动机正式的名字叫 Aho-Corasick 算法,以算法发明人 Alfred V. Aho 和 Margaret J.Corasick 的名字命名。
AC 自动机的构建包含三个步骤: 构建前缀树、计算失配指针、计算后缀匹配项。
我们以 {say, she, shr, he, her} 为例,来看下 AC 自动机的构建和查找过程。
构建前缀树 (Trie)¶
https://zh.wikipedia.org/wiki/Trie
将关键词列表中的关键词逐个字符的加入前缀树。
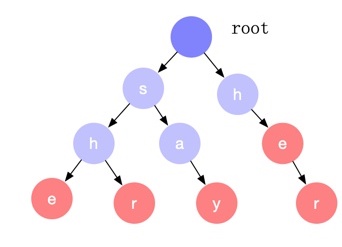
因为前缀树只能顺着某一个路径往下匹配,如果中途遇到不匹配的节点,只能回溯然后从根节点选择另外一个分支继续往下匹配。以处理字符串 sher 为例:首先,我们匹配了 she 子树,下一个字符 r 无法匹配,这时需要回溯到开始,然后从前缀树的根节点再选择 her 分支往下匹配。但是观察可以发现 her 的前缀 he 是 she 的一个后缀,she 匹配也就意味着 he 已经匹配,我们可以直接跳过 her 子树的 he 匹配,直接从 e 节点开始继续往下匹配,这个横向的跳转就是 失配指针 。
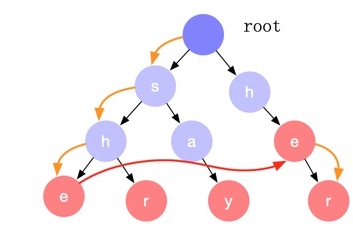
AC 自动机构建的主要过程就是计算失配指针的过程。
计算失配指针¶
AC 自动机的前缀树的节点都存在失配指针,它表示从当前状态节点往下匹配失败后,我们应该跳转到哪个节点继续匹配。如上图中红色的箭头。
失配指针的计算过程如下:
第二层节点的失配指针为根节点。
从第三层开始对前缀树做宽度优先遍历。若当前处理到节点 x,从它的父节点开始沿着失配指针上溯直到根节点,如果中间遇到某个节点存在一个子节点,其字符和节点 x 的相同,那么就将节点 x 的失配指针指向这个子节点。否则失配指针为根节点。
完全计算完成后失配指针如下图所示:
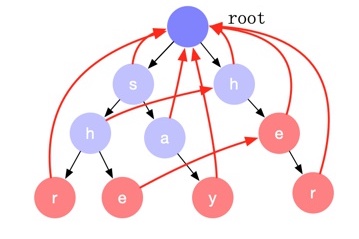
计算后缀匹配项¶
我们看 she 字符串的匹配,当前缀树匹配到 e 这个节点的时候,代表匹配了 she 字符串,但其实 he 这个后缀也是匹配的。也就是说,对于前缀树上的每一个节点,我们除了判断节点本身是否是一个匹配项外,还需要判断其是否存在后缀匹配项。
后缀匹配项的计算方式如下:
宽度优先遍历所有节点,对于每一个节点 x,沿着其失配指针一直回溯直到根节点,中间遇到的节点如果是匹配节点(红色节点),那么这个节点代表的字符串就是节点 x 的一个后缀匹配项。实现中每个节点只需记录一个指向最长后缀匹配项节点的指针即可(下图中的蓝色箭头),查找的时候沿着这个指针上溯即可找到所有的后缀匹配项。
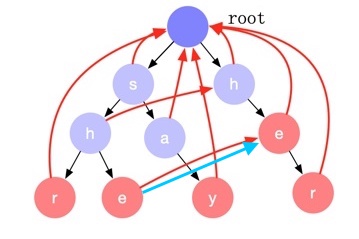
这个算法可以用来解答 Leet#1032 字符流 问题。 解答 。
